Aplicaciones de la elipse

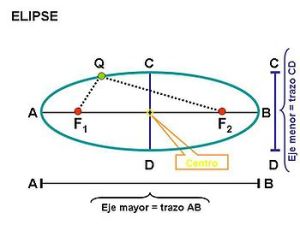
La propiedad óptica de la elipse se aplica en las «galerías de murmullos» como la que se encuentra en el Convento del Desierto de los Leones, cerca de la Ciudad de México, en la cual un orador colocado en un foco puede ser escuchado cuando murmura por un receptor que se encuentre en el otro foco, aún cuando su voz sea inaudible para otras personas del salón. Otra aplicación de la propiedad óptica de la elipse es la de ciertos hornos construidos en forma de elipsoides. Si en uno de sus focos se coloca la fuente de calor y en el otro se coloca el material que se quiere calentar, todo el calor emanado por la fuente de calor se concentrará en el otro foco.

Astronomía

Una de las principales aplicaciones de la elipse se da en la astronomía. Johannes Kepler, estudiando los movimientos de Marte, al aplicar el modelo de Copérnico de órbitas circulares alrededor del sol, vio que los cálculos discrepaban ligeramente de la posición real del planeta en el firmamento. Así que intentó ajustar la órbita a otras curvas y finalmente encontró que la elipse se ajustaba maravillosamente a ella. Así encontró su primera ley del movimiento de los planetas. En realidad Kepler tuvo una suerte enorme, ya que Marte era el planeta conocido entonces cuya órbita era más excéntrica. Si en lugar de Marte hubiera decidido estudiar a Venus, cuya órbita es prácticamente circular, posiblemente nunca hubiera descubierto sus leyes del movimiento.

Las tres leyes sobre el movimiento planetario de Kepler son:

• Los planetas se mueven en órbitas elípticas, uno de cuyos focos es el Sol.
• Los planetas barren áreas iguales en tiempos iguales. Es decir, en la figura , si el tiempo que tarda el planeta en ir de A a B es igual que el que tarda en ir de C a D, entonces el área OAB es igual al área OCD.
• El cuadrado del período de un planeta (el tiempo que tarda en dar una vuelta completa alrededor del sol) es proporcional al cubo de su distancia media (la longitud del semieje mayor de la elipse) al sol.

Kepler encontró sus leyes empíricamente, pero fue Newton, utilizando el Cálculo Diferencial que acababa de inventar, y su modelo de gravitación universal, quien probó dichas leyes.

En la tabla siguiente aparece la excentricidad de las órbitas planetarias, así como la distancia media del planeta al sol medida en unidades astronómicas (U.A.), una unidad astronómica es, por definición, la distancia media de la tierra al sol.

Planeta Excentricidad Distancia media (U.A.) Mercurio 0.206 0.387 Venus 0.007 0.723 Tierra 0.017 1 Marte 0.093 1.52 Júpiter 0.048 5.2 Saturno 0.056 9.54 Urano 0.047 19.18 Neptuno 0.009 30.06 Plutón 0.25 39.44

Si medimos el tiempo que tarda un planeta en dar la vuelta alrededor del sol en años terrestres, la constante de proporcionalidad de la tercera ley de Kepler es 1, es decir, su fórmula es

p2 = a3,

donde p es el período y  a es el radio mayor de la elipse.

Ejemplos

1. 1. Encontrar la diferencia entre el radio mayor y el radio menor de la órbita de la tierra, sabiendo que el radio mayor es aproximadamente de 149,600,000 Km.

Solución

Como la excentricidad de la órbita terrestre es

e = c     a = 0.017

y el radio menor es

b = ( a2-c2) 1/2

entonces c = 0.017a y

b = ( a2( 1-0.0172) ) 1/2 = 0.999855 a = 149,578,308 Km

así que la diferencia entre el radio mayor y el radio menor es

149,600,000-149,578,308 = 21,692 Km

que es menos de dos veces el diámetro de la tierra, es decir, es insignificante comparada con el tamaño de la órbita.

2. Encontrar el período de Urano.

Solución:

La distancia media de Urano al sol es a = 19.18 U.A., así que su período, de acuerdo a la tercera ley de Kepler es p = Ö{19.18³} = 84 años.

No nada más los planetas satisfacen las leyes de Kepler, sino que también todos los cuerpos que giran alrededor de otros, por ejemplo, los cometas girando alrededor del sol, los satélites girando alrededor de los planetas, y aún el sistema solar girando alrededor del centro de la Vía Lactea. La constante de proporcionalidad de la tercera ley depende básicamente de la masa del cuerpo central.

 

---

Referencias

[1]

E. de Oteyza, E. Lam, J.A. Gómez, A. Ramirez, C. Hernández, «Geometría Analítica», Prentice-Hall Hispanoamericana, S.A., México, 1994.

[2]

E. Purcell, D.Varberg, «Cálculo con Geometría Analítica», Prentice-Hall Hispanoamericana, S.A., México, 1993.

[3]

M. Sullivan, «Trigonometría y Geometría Analítica», Prentice-Hall Hispanoamericana, S.A., México, 1997.

Elipse

Se llama elipse  al lugar geométrico  de un plano, cuya suma de distancias a dos puntos fijos llamados  focos es constante

Según la definición , si Fy F’ son los puntos fijos en el plano , llamados focos  de la elipse , y P  es un punto  cualquiera de la elipse , la suma de las distancias PF’y Pf  es constante , Si designamos por 2ª ala cantidad constante , es decir : PF’ +PF =2ª Con a>O la recta que une  los focos  es el eje de simetría de la elipse . si P’ es el simétrico de P respecto  ala recta FF’ , este será la mediatriz del segmento pp’ y se verifican las siguientes igualdades .P’F’= PF’ Y P’F de donde P’F’ =P’f=2a

Elementos de la elipse

Elementos de la elipse Puntos de una elipse

Si F₁ y F₂ son dos puntos del plano y d es una constante mayor que la distancia F₁ F₂, un punto Q pertenecerá a la elipse, si:

donde es el semieje mayor de la elipse.

[editar] Ejes de una elipse

Eje mayor (2 a) es la distancia mayor entre dos puntos adversos. En la figura, longitud del segmento AB.
La medida a es la mitad del eje mayor, o sea es el semieje mayor. La distancia del centro de la elipse al punto A o al punto B.

El resultado constante de la suma de las distancias de cualquier punto a los focos equivale al eje mayor.
Obsérvese que d(AF₂) + d (AF₁) = d(AF₂) + d (BF₂)= AB

La medida b es la mitad del eje menor, o sea es el semieje menor, la distancia del centro al punto C o al punto D.

[editar] Excentricidad de una elipse

La excentricidad de una elipse es la razón entre su semidistancia focal (segmento que va del centro de la elipse a uno de sus focos), denominada por la letra ‘c’, y su semieje mayor. Su valor se encuentra entre cero y uno.

, con (0 < e < 1)

Dado que , también vale la relación:

o el sistema:

La excentricidad indica la forma de una elipse; una elipse será más redondeada cuanto más se aproxime su excentricidad al valor cero.^[3]

Ecuaciones de la elipse

La ecuación de una elipse en coordenadas cartesianas, con centro en el origen, es:

donde a > 0 y b > 0 son los semiejes de la elipse (a corresponde al eje de las abscisas, b al eje de las ordenadas). El origen O es la mitad del segmento [FF’]. La distancia entre los focos FF’ se llama distancia focal y vale 2c = 2ea, siendo e la excentricidad y a el semieje mayor.

Si el centro de la elipse se encuentra en el punto (x₁, y₁), la ecuación es:

En coordenadas polares con origen en un de sus focos la ecuación de la elipse es:

En coordenadas polares con origen en su centro la ecuación de la elipse es:

La ecuación paramétrica de una elipse con centro en (h,k) es:

con no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre α y θ es

.

[editar] Área interior de una elipse

El área de la superficie interior de una elipse es:

Siendo a y b los semiejes.^[4]

[editar] Longitud de una elipse

El cálculo del perímetro de una elipse requiere del cálculo de integrales elípticas de segunda especie.

Sin embargo, el matemático Ramanujan ideó una ecuación más simple que se aproxima razonablemente a la longitud de la elipse, pero en grado menor que la obtenida mediante integrales elípticas. Ramanujan, en su formula, entre otros valores utiliza el “semieje mayor” y el “semieje menor”. Ecuación de la longitud de una elipse:

[editar] Propiedades notables

La elipse goza de ciertas propiedades asociadas a sus componentes, como se puede ver en Analogía de Michelson y Morley.

[editar] La elipse como cónica

La elipse surge de la intersección de una superficie cónica con un plano, de tal manera que la inclinación del plano no supere la inclinación de la recta generatriz del cono, consiguiendo así que la intersección sea una curva cerrada. En otro caso el corte podría ser una hipérbola o una parábola. Es por ello que a todas estas figuras bidimensionales se las llama secciones cónicas o simplemente cónicas.

la elipse como conica.

[editar] La elipse como hipotrocoide

La elipse es un caso particular de hipotrocoide, donde R = 2r, siendo R el radio de la circunferencia directriz, y r el radio de la circunferencia generatriz.

En una curva hipotrocoide, la circunferencia que contiene al punto generatriz, gira tangencialmente por el interior de la circunferencia directriz.

La elipse como caso particular de hipotrocoide. Datos: R = 10, r = 5, d = 1.

[editar] Construcción paramétrica de una elipse

Se dibujan dos circunferencias concéntricas cuyos diámetros equivalen a la medida de los ejes ortogonales de la futura elipse. Si trazamos segmentos palalelos a los ejes principales X e Y, partiendo del extremo de los radios alineados, la intersección de dichos segmentos son puntos de la elipse.

[editar] Anamorfosis de un círculo en una elipse

Artículo principal: Anamorfosis

Cierta trasformación de la circunferencia (al deformar ortogonalmente el plano cartesiano asociado a ella), se denomina anamorfosis. Se corresponde a una perspectiva especial. El término anamorfosis proviene del idioma griego y significa trasformar.

Una circunferencia en un plano cartesiano no deformado.

Esta circunferencia se transforma en una elipse mediante una anamorfosis, donde el eje Y se ha contraído y el X se ha dilatado.

En el caso de la circunferencia, si el plano cartesiano se divide en cuadrados, cuando dicho plano se «deforma» en sentido del eje X, el Y, o ambos, la circunferencia se transforma en una elipse, y los cuadrados en rectángulos.

VIDEO DE COORDENADAS POLARES

Division de un segmento en una razon dada

cono cien do la coordenada del punto p1(X1, Y1) y las coordenadas del punto P2 ( X2 ., Y2 v) hallando se  las coordenadas de un tercer punto

 P ( X, y)que divide al segmento p1p2

 de tal modo que la razon m/ n= r

desde los puntos p1,p,p2 un juego  de rectas perpendiculares a los ejes coordenados , siendo Q y R  sus puntos de interseccion

plano cartesiano

Se llama plano cartesiano en honor a Rene Descartes  el plano cartesiano  se forma al trazar dos rectas perpendiculares XX e YY que se cortan en un punto llamado «origen».

 los ejes XX e YY se llaman coordenadas y dividen al´plano en 4 regiones llamadas cuadrantes .

SISTEMA DE COORDENADAS RECTANGULARES

SISTEMA DE COORDENADAS RECTANGULARES

Sistema de coordenadas rectangulares

En este sistema para localizar un punto en el plano utilizaremos como referencia dos rectas perpendiculares una horizontal(eje de abscisas) y otra vertical (eje de ordenadas )
que se cortan en un punto
llamado origen, y a los ejes se les asocia una escala numérica .

foto de coordenadas

coordenadas

l sistema de coordenadas polares es un sistema de coordenadas bidimensional en el cual cada punto o posición del plano se determina por un ángulo y una distancia.

De manera más precisa, todo punto del plano corresponde a un par de coordenadas (r, θ) donde r es la distancia del punto al origen o polo y θ es el ángulo positivo en sentido antihorario medido desde el eje polar (equivalente al eje x del sistema cartesiano). La distancia se conoce como la «coordenada radial» mientras que el ángulo es la «coordenada angular» o «ángulo polar».

En el caso del origen de coordenadas, el valor de r es cero, pero el valor de θ es indefinido. En ocasiones se adopta la convención de representar el origen por (0,0º).